
Where the summation is usually taken over all the reflections giving significant intensities.
This is done by calculating a reliability index or R factor defined by Since the phases cannot be compared with any observable quantities, the validity of the proposed structure must be tested by comparison of the calculated values of the amplitudes of the structure factor F c with the observed amplitudes | F 0|. It will be seen that it is possible to calculate simultaneously both the amplitude and phase of each beam that would be diffracted by the proposed structure. Apart from the direct methods of obtaining some initial phases, both the solution and refinement processes depend on the ability to calculate structure factors for a proposed approximate arrangement of some or all of the atoms in the crystal structure. The solution of a crystal structure therefore consists of applying some technique for obtaining the approximate phases of at least some of the X-ray reflections, and the process of structure refinement is one in which the knowledge of phases is extended to all reflections and is made as accurate as possible for all reflections. This constitutes what is known as the phase problem in crystallography. So two of the three necessary pieces of information about each beam are known, but unfortunately there is no method available yet for observing the phase of each diffracted beam, which is the third piece of information needed before mathematical recombination is possible to produce an image of the structure. From the measured intensity of the beam its amplitude may readily be deduced. By identifying the Miller indices ( hkl) of the crystal plane giving rise to each diffracted beam, the direction of the beam is specified. In X-ray crystallography, the diffracted beams are separately observed and their intensities measured as the blackness of spots on an X-ray film or by direct quantum counting in a diffractometer. In the physical recombination of rays by the lenses of a microscope these three pieces of information about each ray are retained and used automatically in the recombination process. The way in which the separate scattered or diffracted rays combine to form an image depends on three factors associated with each ray: (a) the direction, (b) the amplitude, (c) the phase. In a microscope this recombination is done physically by the lenses of the microscope but in crystallography the corresponding recombination of diffracted beams must be done by mathematical calculation. This image is the crystallographic analogue of the image formed in a microscope by recombination of the rays scattered by the object. The set of structure factors for all the reflections hkl are the primary quantities necessary for the derivation of the three-dimensional distribution of electron density, which is the image of the crystal structure, calculated by Fourier methods.
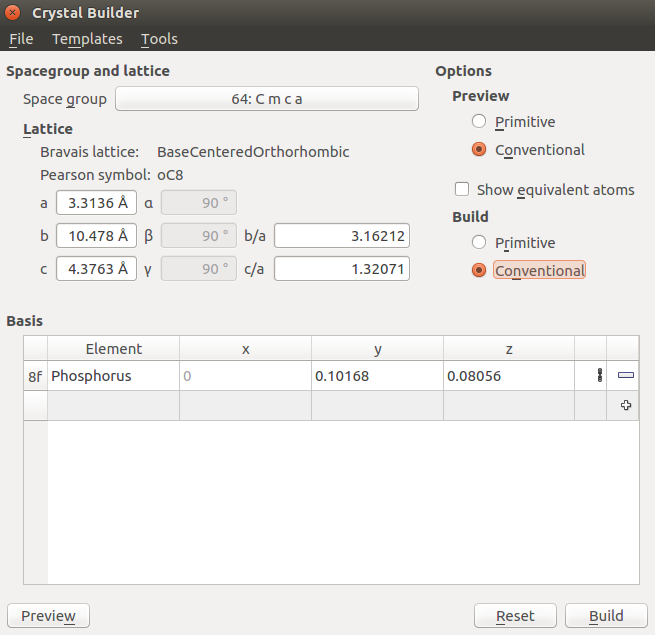
It plays a central role in the solution and refinement of crystal structures because it represents the quantity related to the intensity of the reflection which depends on the structure giving rise to that reflection and is independent of the method and conditions of observation of the reflection. In X-ray crystallography the structure factor F( hkl) of any X-ray reflection (diffracted beam) hkl is the quantity that expresses both the amplitude and the phase of that reflection. Introduction to the calculation of structure factors S.


 0 kommentar(er)
0 kommentar(er)
